Puncturable Encryption – A Fine-Grained Approach to Forward-Secure Encryption and More: Part I
This series of blog posts provides an introduction to the recent concept of puncturable encryption (PE), presents state-of-the-art research on PE schemes and discusses implementation aspects for applications. Loosely speaking, PE is a variant of public-key encryption (PKE) that allows realizing the property of fine-grained forward security. We recall that in a PKE scheme, an adversary that gets access to the secret key immediately has the power to decrypt all ciphertexts ever produced concerning the corresponding public key (be it in the past or the future). Forward security of a PKE scheme now means that if the secret key leaks, it is still possible to protect the confidentiality of old ciphertexts which reduces the damage associated with key leakage.
In the first part of this blog series, we will cover the motivation of forward security and give well-known approaches for forward-secure public-key encryption. In Part II, we will clarify how PE makes this concept fine-grained and also present state-of-the-art research on PE schemes (specific variants of PE, Bloom-Filter Encryption and Ciphertext-Puncturable Encryption). Finally, in Part III, we discuss some interesting applications (0-RTT forward-secure key exchange for TLS, Cloudflare's Geo Key Manager and SafetyPin) as well as talk about the implementation aspects.
Motivating Forward Security
Leakage of secret keys is a major security risk in modern systems and cryptographic protocols, especially if the same secret key is used for a longer period of time. There is a multitude of potential attack vectors, ranging from insufficient key-management practices to more sophisticated attack methods that rely on side-channels. Latter attacks use signals that vary with the use of the secret key to non-invasively extract the secret key. They range from power consumption over electromagnetic radiation to timing measurements (such as cache accesses) and are a threat to chips used in smart cards or related hardware tokens to large systems such as servers (running in the cloud).
Especially due to the increasing reliance on cloud services, for server machines that keep secret keys in software or trusted execution environments (TEEs) like ARM’s TrustZone or the increasingly popular SGX by Intel such aforementioned attacks pose a serious problem. Especially within heavily virtualized environments, it is well known that the shared resources introduce the danger of information leakage, i.e., extracting secret keys held in shared memory, e.g., via co-located virtual machines controlled by an attacker [RTSS09,ZJRR12,ZJRR14]. Moreover, micro-architectural attacks such as the already mentioned cache attacks (against TEEs) are getting increasingly sophisticated and more devastating (cf. [SG20]). While rotating keys frequently helps to reduce the risk, frequently deploying new keys may soon become impractical if the frequency gets too high.
Forward security has been traditionally an important property in interactive key-exchange protocols and meanwhile is mandatory in TLS 1.3 via the exclusive use of Ephemeral Diffie-Hellman (DHE). Besides other strong properties such as post-compromise security, it is considered an important security property in major secure-messaging applications such as Signal and WhatsApp. Furthermore, it is an integral part of common protocols such as the Google's Application Layer Transport Security (ALTS) protocol, the SSH protocol, or the key-exchange protocol underlying WireGuard's VPN. Forward security can in general be efficiently obtained in protocols such as the aforementioned where interaction is allowed, intuitively as switching or updating keys can be part of the protocol. However, it gets more involved when considering this property for non-interactive primitives such as public-key encryption where public keys should be static over a longer period of time and interaction is not possible or desirable. For a detailed discussion about forward security in general, we recommend to take a look at [BG20].
Forward Security in Public-Key Encryption
Forward security in public-key encryption mitigates the problems associated with the leakage of a secret key \(sk\) corresponding to a long-term public key \(pk\) in the sense that the confidentiality of the data encrypted in old ciphertexts is still protected after a key is leaked. The basic idea is to discretize time into epochs (or intervals), compute ciphertexts concerning the current epoch \(i\) and while there is a fixed public key over a potentially long period of time, the secret key evolves over time. This evolution of the secret key updates the secret key, deletes the old secret key, and the update is realized in a way that a leaked secret key in interval \(i\) is no longer useful to decrypt ciphertexts produced in any interval \(j < i\).
The idea is illustrated in Figure 1 below and it is important to note that ideally, the public and the secret keys are compact, i.e., at least only sub-linearly dependent and ideally independent of the maximum number of epochs. It is not hard to see that a scheme where the keys are linear in the size of the maximum number \(n\) of epochs is rather easy to devise. Therefore, we set the public key to be a sequence \((pk_1,\ldots,pk_n)\) of \(n\) independently generated public keys, use the \(i\)'th public key in epoch \(i\) and evolving the secret key to epoch \(i+1\) simply means deleting the \(i\)'th secret key. While such a scheme can work for very small \(n\), it soon gets impractical as \(n\) gets reasonably large. One way to compress the public key is to rely on identity-based encryption (IBE) by using, e.g., the Boneh-Franklin IBE [BF01], where the public key \(pk\) is independent but the secret keys \((sk_1,\ldots,sk_n)\) are linearly in the maximum number of epochs \(n\) (essentially, each epoch \(i\) has its own epoch-identity key \(sk_i\) and one encrypts towards “identity” \(i\)).
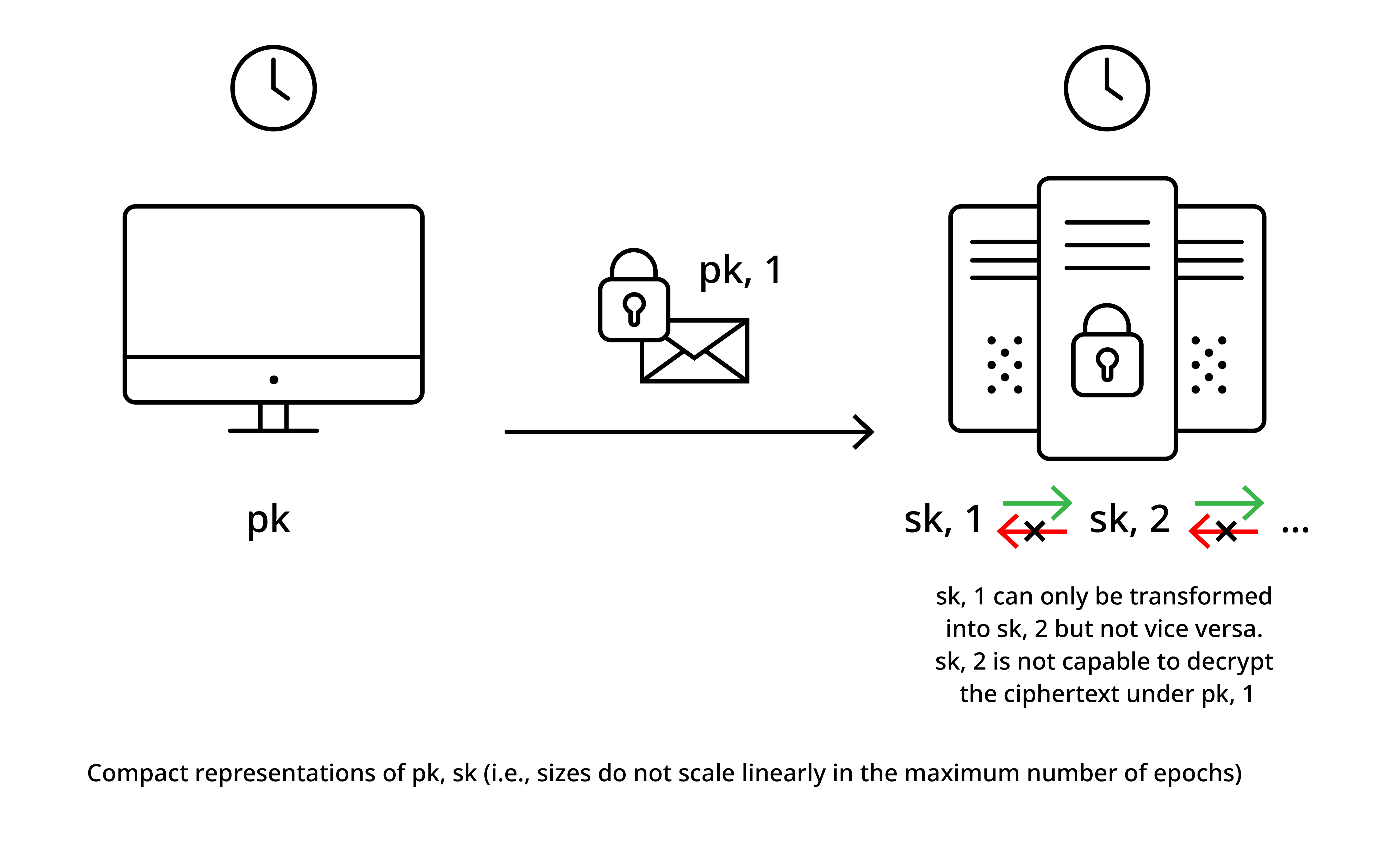
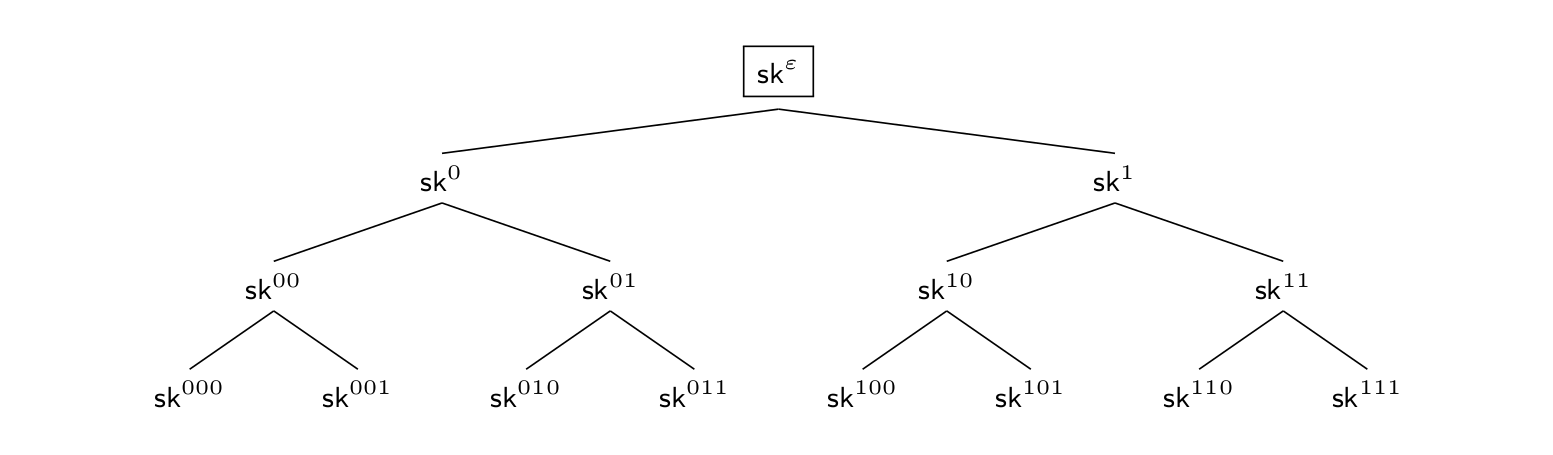
Devising a scheme for virtually unbounded \(n\) with compact public and secret keys is more tricky and has for the first time been proposed by Canetti, Halevi and Katz (CHK) [CHK03]. The basic idea is to rely on a binary tree-based approach and in particular the approach of hierarchical identity-based encryption (HIBE). Roughly speaking, in a HIBE, one encrypts for an identity \(id\) and from a compact main secret key one can derive secret keys for any identity. Having a secret key for some identity \(id\) allows to delegate the secret key for any identity with prefix \(id\). However, the other direction is not possible, i.e., one can only delegate for extended identities but not compute secret-key material for prefixes of them. As a more concrete example, let us assume a binary-identity space \(\{0,1\}^\ell\) (with \(\ell\) being the height of the binary tree). Now, having a secret key for identity \(0\) lets us compute a secret key for any identity \(0\{0,1\}^{\ell-1}\) while from a secret key for identity \(1\) we can derive a secret key for any identity \(1\{0,1\}^{\ell-1}\) (CHK actually use a relaxed version of a HIBE called binary-tree encryption (BTE), which however is basically a HIBE with the aforementioned identity space).
In Figure 2, we provide an illustrative example of such a HIBE with identity space \(\{0,1\}^3\) and where the main secret key is denoted as \(sk^\varepsilon\). For a forward-secure PKE, let us now consider all the secret keys at the leaves to represent the epoch keys, i.e., we have eight epochs.
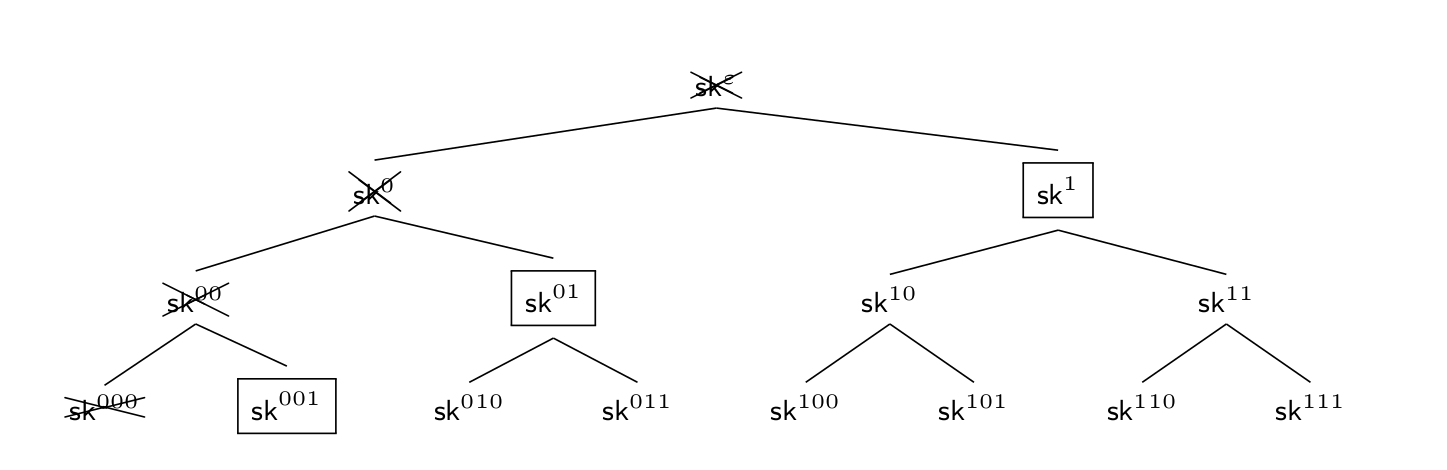
In the first epoch, all ciphertexts are now computed for identity \(000\) and initially the secret key (boxed) is \(sk^\varepsilon\) which allows to derive all secret keys in the tree. Let us now see what happens when we evolve the secret key to the next (second) epoch represented by identity \(001\), which we illustrate in Figure 3. The idea is that one stores as the secret key (boxed) all secret keys representing siblings on the path from the secret key of identity \(000\) to the root which allow to derive all the remaining secret keys and deletes the elements that would allow deriving the secret key for the identity of the previous epoch (i.e., \(sk^{000}\)). This procedure can now be repeated when evolving the secret key to the next epochs.
For a concrete instantiation, this typically means that the public key of the respective forward-secure PKE scheme is logarithmic in the maximum number of epochs and can be made constant using a random oracle (a significant improvement over the naive linear-sized example mentioned before), secret keys are logarithmic and the size of the ciphertext can ideally be constant when using a suitable HIBE scheme [BBG05].
Obviously, if the switches between intervals happen too frequently, it requires good synchronization, whereas for longer time intervals, a looser synchronization (which is desirable) is sufficient. Nevertheless, the achieved forward-security property is very coarse-grained, i.e., in case of secret-key leakage, all ciphertexts within the current interval are not protected.
In the next blog post (Part II), we discuss how to add the fine-grained PE approach to forward-secure PKE and discuss state-of-the-art PE research. If you have any comments, suggestions or questions, please feel free to contact us (@drl3c7er, @CStriecks, @sebastinas_).
References
- [BBG05]: Dan Boneh, Xavier Boyen, Eu-Jin Goh: Hierarchical Identity Based Encryption with Constant Size Ciphertext. EUROCRYPT 2005
- [BF01]: Dan Boneh, Matthew K. Franklin: Identity-Based Encryption from the Weil Pairing. CRYPTO 2001.
- [BG20]: Colin Boyd, Kai Gellert: A Modern View on Forward Security. The Computer Journal, 2020.
- [CHK03]: Ran Canetti, Shai Halevi, Jonathan Katz. A forward-secure public-key encryption scheme. EUROCRYPT 2003
- [RTSS09]: Thomas Ristenpart, Eran Tromer, Hovav Shacham, and Stefan Savage: Hey, you, get off of my cloud: exploring information leakage in third-party compute clouds. In ACM CCS 2009.
- [SG20]: Michael Schwarz, Daniel Gruss. How trusted execution environments fuel research on microarchitectural attacks. IEEE Security Privacy, 18(5):18–27, 2020.
- [ZJRR12]: Yinqian Zhang, Ari Juels, Michael K. Reiter, and Thomas Ristenpart. Cross-vm side channels and their use to extract private keys. In ACM CCS 2012.
- [ZJRR14]: Yinqian Zhang, Ari Juels, Michael K. Reiter, and Thomas Ristenpart. Cross-tenant side-channel attacks in paas clouds. In ACM CCS 2014.



